分类 V2X 下的文章

“车联网（Vehicle-to-everything）：汽车和其他相关设备的通讯。车联网（Vehicle-to-everything）简称V2X，是将汽车和其他车辆或是可能影响汽车的设备所进行的通信。车联网是包括其他种类通信的汽车通信系统，其他的通信有V2I（汽车对基础设施、汽车对道路系统）、V2N（汽车对网络）、V2V（汽车对汽车）、V2P（汽车对行人）、V2D（汽车对设备）。”

蝴蝶密钥扩展（ButterflyExpansion）算法，用于为车辆持续生成PC证书。中国的CCSA标准《基于LTE的车联网无线通信技术 安全证书管理系统技术要求》使用了该算法。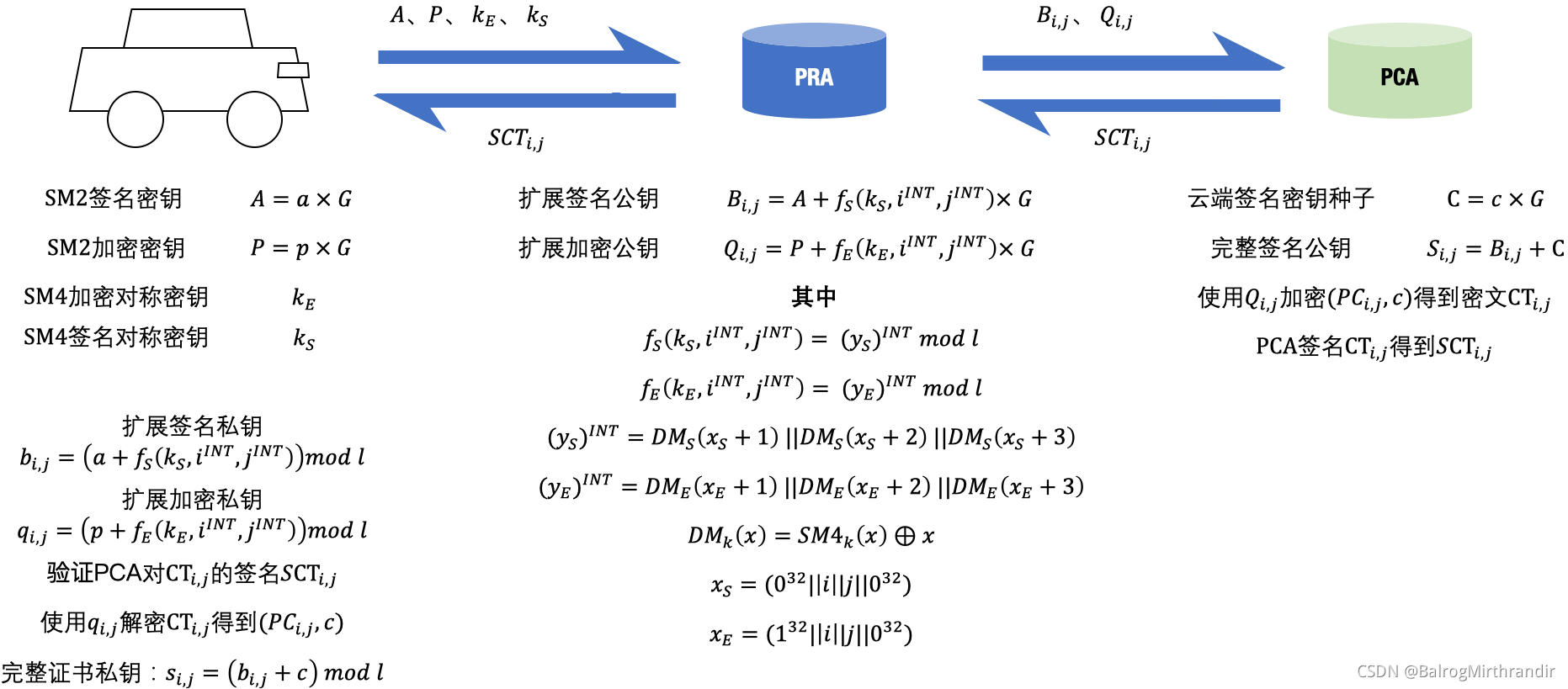
bufferflyexpansio.png
在假名证书申请流程和下载流程的基础上，密钥衍生的补充流程如下，本标准对密钥衍生流程中所使用的算法提出了一种建议：

  • 1) V2X设备在生成PC申请请求时，使用非对称密钥算法生成两对种子公私密钥对：签名密钥对(a, A)，和加密密钥对(p, P)；并使用对称密钥算法生成两个对称密钥：签名对称密钥kS和加密对称密钥kE；
  • 2) V2X设备发送给PRA的PC申请请求中，包括了A、P、kS、kE；
  • 3) PRA对PC申请请求、EC证书或令牌等信息校验通过后，使用A、P、kS、kE进行第一轮扩展运算，公钥因子A与kS进行扩展计算，得到签名扩展公钥B，P与kE进行扩展计算，得到加密扩展公钥Q；如此进行若干轮扩展运算，得到(Bi,j,Qi,j)；
  • 4) PRA向PCA发送PC签发请求时，将(Bi,j, Qi,j)逐一发送给PCA，用于签发批量的PC；
  • 5) PCA签发PC证书前，随机生成1对公私钥对(c, C)，其中公钥分量C与若干个Bi,j逐一进行运算，得到完整公钥Si,j；
  • 6) PCA基于Si,j构造的ToBeSignedCertificate进行签发得到假名证书PCi,j，再用对应的Qi,j对PCi,j及c进行加密，对该密文使用PCA的私钥进行签名；
  • 7) PCA返回批量PC证书至PRA时，将若干个密文发送至PRA，PRA检查并筛选出该V2X设备对应的若干个密文消息，将其打包为PC证书下载应答；
  • 8) V2X设备收到PRA返回的PC证书下载应答后，使用步骤1)中生成的a和p，分别与kS和kE进行若干轮计算，得到bi,j和qi,j；
  • 9) 验证步骤5)中PCA签名的有效性，验证通过后，再使用qi,j解密对应的密文，得到PCi,j及c,最终使用bi,j与c计算得到PCi,j所对应的完整私钥si,j。
  • 注1： 下标(i,j)表示单个的假名证书所对应的i和j的组合。其中i为该假名证书所对应的周期，j为该假名证书在当前周期中对应的序号。
  • 注2： 以上所述“签名”的种子密钥对（公钥因子、私钥因子）、对称密钥、扩展密钥，用于衍生V2X设备假名证书PC内的完整公钥和对应的完整私钥。
  • 注3： 以上所述“加密”的种子密钥对（公钥因子、私钥因子）、对称密钥、扩展密钥，用于衍生一对公私钥，对PCA返回至V2X设备的PC证书等消息进行加密、解密。
    密钥衍生函数

符号表达说明
有一个公认的“基点”，表示为G；
椭圆曲线的阶数用l表示；
对于一个比特串b和数字n，bn表示通过将比特串b重复n次而形成的比特串；
对于比特串x，xINT表示x转换为整数，例如：如果x = 0101，则xINT = 5；
对于比特串x和数字n，x + n是xINT + n产生的比特串的简写，例如：如果x = 0100，则x + 1 = 0101，x + 2 = 0110，x + 3 = 0111，依此类推；
对于比特串x和y，x ⊕ y表示它们的按位异或，而x || y表示串联的比特串，例如：如果x = 0110且y = 1010，则x ⊕ y = 1100且x || y = 01101010；
对于128比特字符串k和m，Symm (k, m)表示使用对称加密算法得到的128比特密文，m为被加密的明文数据，k为对称密钥，使用128比特的分组大小；
对于数字m和n，m mod n表示对具有模数n的m进行模运算的结果，例如：如果m = 9且n = 2，则m mod n = 1。
密钥衍生函数
2个密钥衍生函数：签名函数fS和加密函数fE。2个函数的参数如下：

  • 对称加密算法Symm，具有128比特的输入和输出以及128比特的密钥，采用SM4分组密码算法，ECB/NoPadding工作模式。
  • 一个128比特的密钥，分别表示为fS函数的kS，和fE函数的kE。
  • l是一个256比特的整数，表示进行密钥衍生的椭圆曲线的基点的阶。
    两个函数的输入为(iINT, jINT)两个整数，其范围是(0 , 232-1)。

两个函数的输出为一个256比特的整数o，范围为(0 , l)。
两个函数过程如下：

  • a）将输入iINT和jINT转换为32比特的比特串i和j。
  • b）拼接下列128位的比特串xS（用于fS）或xE（用于fE）。
  • 1）xS = (032 || i || j || 032)
  • 2）xE = (132 || i || j || 032)
  • c）创建如下的临时输出yS（用于fS）或yE（用于fE）。输出为3×128 = 384比特的字符串。
  • 1）yS = (Symm(kS, xS+1)⊕(xS+1)) || (Symm(kS, xS+2)⊕(xS+2)) ||(Symm(kS, xS+3)⊕(xS+3))
  • 2）yE = (Symm(kE, xE+1)⊕(xE+1)) || (Symm(kE, xE+2)⊕(xE+2)) ||(Symm(kE, xE+3)⊕(xE+3))
    这里，“x + i”表达了“将八位位组字符串x转换为整数，该整数加i，然后将加了i之后的整数转换回八位位组字符串”。例如，如果xS = (032 || i || j || 032) = (0000 0000 0000 0000 0000 0000 0000 0000b || i || j || 0000 0000 0000 0000 0000 0000 0000 0000) ，则xS + 2 = (0000 0000 0000 0000 0000 0000 0000 0000 b || i || j || 0000 0000 0000 0000 0000 0000 0000 0010)
  • d）fS和fE的最终输出如下：
  • 1）fS(kS, iINT, jINT) = ySINT mod l
  • 2）fE(kE, iINT, jINT) = yEINT mod l

相关：
https://blog.csdn.net/zhushuanghe/article/details/121169472

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5